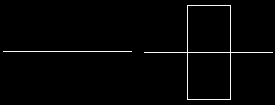Prendiamo
un segmento e raddoppiamo la sua lunghezza.
Otteniamo due copie del segmento originale.
2=21
In generale otteniamo tante copie quanto è il numero di
ingrandimenti.
Si ha che f(n) = n.
Dunque d=1
|
|
| |
Figura 1 |
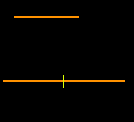
Prendiamo ora un rettangolo e raddoppiamo la lunghezza di entrambe le sue dimensioni.
Otteniamo quattro copie dell'originale.
4=22
|

|
| |
Figura 2 |
Se triplichiamo la lunghezza di entrambe le sue dimensioni otteniamo invece nove copie dell'originale. 9=32
In generale otteniamo che le copie sono uguali al quadrato del numero di ingrandimenti.
Si ha che f(n) = n2
Dunque d=2
|

|
| |
Figura 3 |
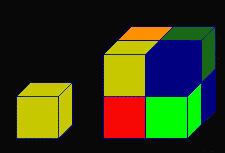
Prendiamo un cubo e raddoppiamo la lunghezza del suo lato.
Otteniamo così otto copie dell'originale. 8=23
Se quadruplicassimo la lunghezza del lato, otterremmo ben sessantaquattro copie dell'originale! 64=43
In generale otteniamo che le copie sono uguali al cubo del numero di ingrandimenti.
Si ha che f(n) = n3
Dunque d=
3 |
|
| |
Figura 4 |
Nel caso dei frattali possiamo calcolare la dimensione, tenuto conto
della loro autosimilarità, applicando la
definizione nel passaggio fra il passo iniziale ed il primo passo: ad esempio, nel caso della
curva di Koch,
vediamo che abbiamo 4 segmenti ognuno di lunghezza=1/3 della precedente.
Dunque la dimensione è log(4)/ log(3)
≈ 1.26
La curva di Koch è più di una linea e meno di una superficie!
|
|
| |
Figura 5 |
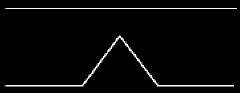
Nel caso del
frattale di Cantor abbiamo invece 2 segmenti ognuno di
lunghezza = 1/3 della precedente.
Dunque la dimensione è log(2)/log(3)
≈
0.63
Il frattale di Cantor è meno di una linea!
|
 Nel caso del
frattale di
Peano abbiamo 9 segmenti ciascuno di lunghezza uguale ad 1/3 del
segmento di partenza. La dimensione frattale è quindi (log9/log3) = 2.
Dunque il frattale di Peano ha la dimensione di una superficie. |
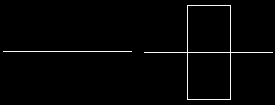 | |
| | |